Understanding the Leading Coefficient Test: A Guide to Polynomial Behavior

The Leading Coefficient Test is a cornerstone concept in mathematics, providing a powerful tool for predicting the end behavior of polynomial functions. By focusing on the leading term, this test enables us to understand how a polynomial behaves as $x \to \pm\infty$. Whether you're graphing equations, analyzing scientific data, or solving engineering problems, mastering this test is essential.

---

What is the Leading Coefficient Test?

The Leading Coefficient Test is a systematic method for analyzing the end behavior of polynomial functions. By examining the leading term—the term with the highest power of $x$—and its coefficient, this test helps predict how the graph behaves as $x \to \infty$ or $x \to -\infty$.

Key Concepts:

• Leading Term: The term with the highest degree (e.g., $ax^n$).
• Leading Coefficient: The coefficient of the leading term ($a$).
• Degree: The highest power of $x$ in the polynomial ($n$).

---

How the Leading Coefficient Test Works

The Leading Coefficient Test revolves around two factors:

1. Degree of the Polynomial ($n$): Determines if the polynomial is odd or even.
2. Sign of the Leading Coefficient ($a$): Indicates whether the graph opens upwards or downwards.

Rules for the Leading Coefficient Test:

1. Even Degree:
   • $a > 0$: Both ends of the graph rise (U-shaped curve).
   • $a < 0$: Both ends of the graph fall (inverted U-shaped curve).
2. Odd Degree:
   • $a > 0$: Falls on the left, rises on the right.
   • $a < 0$: Rises on the left, falls on the right.

---

Examples of the Leading Coefficient Test

Example 1:

Polynomial: $f(x) = 4x^3 - 6x^2 + x - 5$

• Leading Term: $4x^3$
• Degree: $3$ (odd)
• Leading Coefficient: $4 > 0$

Conclusion: The graph falls on the left and rises on the right as $x \to \pm\infty$.

Example 2:

Polynomial: $g(x) = -5x^6 + 3x^5 - x^4 + 2$

• Leading Term: $-5x^6$
• Degree: $6$ (even)
• Leading Coefficient: $-5 < 0$

Conclusion: The graph falls on both ends as $x \to \pm\infty$.

---

Applications of the Leading Coefficient Test

1. Graphing Polynomial Functions

This test provides a starting point for sketching polynomial graphs by determining the general shape and direction.

2. Data Analysis and Modeling

In fields like economics and environmental science, this test helps predict trends such as population growth or resource depletion.

3. Physics and Engineering

Engineers use this test to analyze mechanical systems, such as understanding forces in polynomial relationships.

4. Optimization Problems

The Leading Coefficient Test aids in predicting outcomes in systems described by polynomial equations.

5. Education

Teachers use this test to introduce students to polynomial functions, laying the foundation for calculus and advanced math.

---

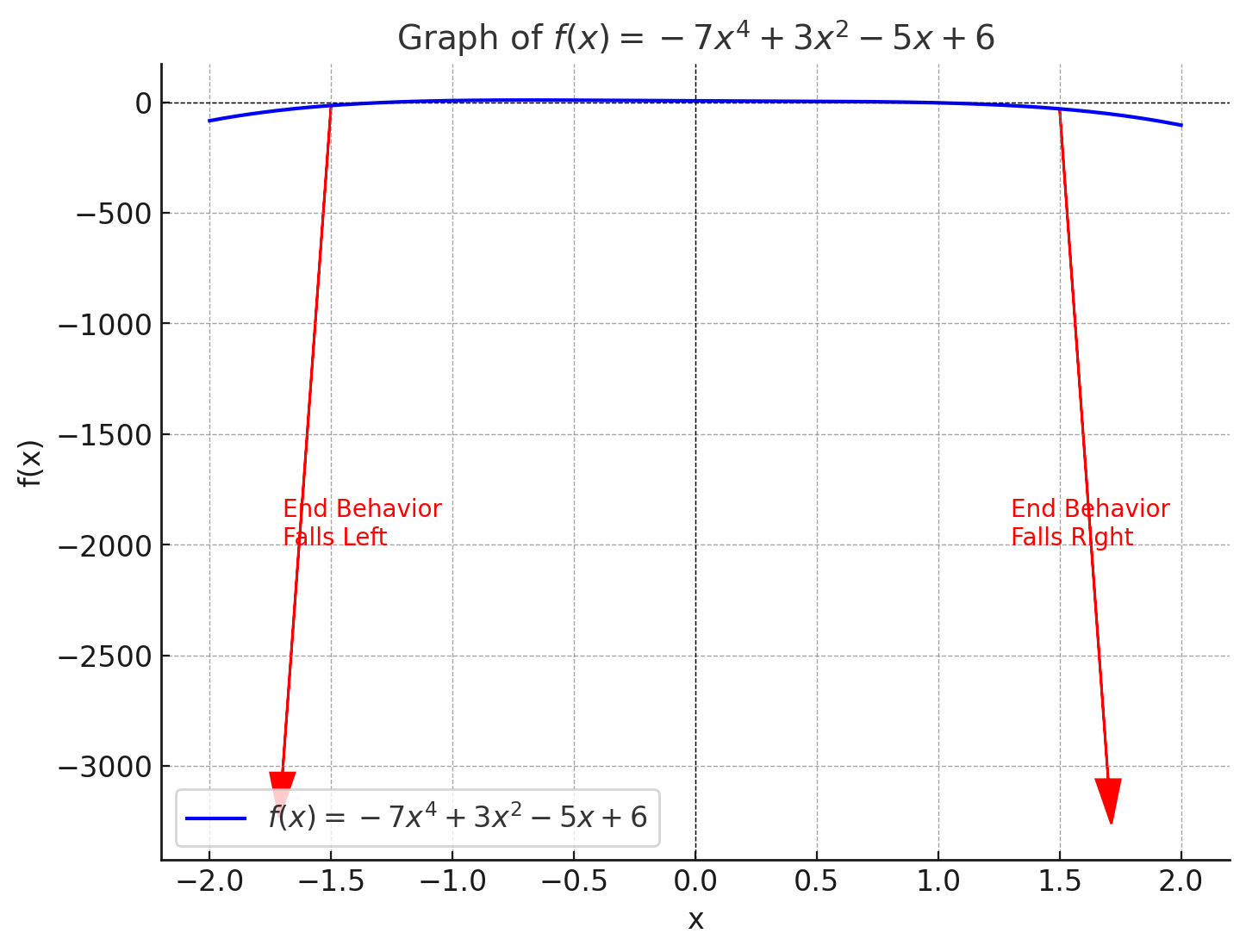
Practice Problem

Problem: Determine the end behavior of $f(x) = -7x^4 + 3x^2 - 5x + 6$.

Solution:

• Leading Term: $-7x^4$
• Degree: $4$ (even)
• Leading Coefficient: $-7 < 0$

Conclusion: The graph falls on both ends as $x \to \pm\infty$.

---

Why the Leading Coefficient Test is Important

The Leading Coefficient Test simplifies complex polynomial problems by focusing on the leading term and its coefficient. It equips you with the ability to make precise predictions about polynomial behavior, bridging theoretical math with real-world applications. From graphing equations to solving engineering challenges, mastering this test is essential for students, educators, and professionals alike.