The Integral of Absolute Value

The Integral of Absolute Value: A Step-by-Step Guide

The integral of absolute value is a fundamental concept in calculus that students often find challenging. Understanding how to handle the absolute value function inside an integral can significantly improve your problem-solving skills. In this article, we’ll walk through the essential steps for solving these types of integrals, provide examples, and break down the key concepts you need to know.

As an academic expert with years of experience helping students like you, I can assure you that with the right approach, you can easily master the integral of absolute value. So, let’s dive into it!

What Is the Absolute Value Function?

The absolute value of a number or function is defined as the distance between that number or function and zero, regardless of whether the number is positive or negative. Mathematically, this is expressed as:

$$|f(x)| = \begin{cases} f(x) & \text{if } f(x) \geq 0 \\ -f(x) & \text{if } f(x) < 0 \end{cases}$$

This piecewise definition is crucial when calculating the integral of absolute value. It essentially means that the absolute value function can be broken into different parts, depending on whether the argument inside the absolute value is positive or negative.

How to Integrate the Absolute Value Function

When you encounter an integral with the absolute value, you must break the integral into separate parts, each corresponding to intervals where the function inside the absolute value is either positive or negative.

Steps to Solve the Integral of Absolute Value:

1. Identify where the function changes sign.
   This is where the function inside the absolute value is equal to zero. These points will divide your integral into separate intervals.

2. Rewrite the integral without the absolute value.
   Use the piecewise definition of the absolute value to rewrite the integral over each interval where the function’s sign is consistent.

3. Evaluate the integrals for each piece.
   Integrate each part of the function separately, then combine the results.

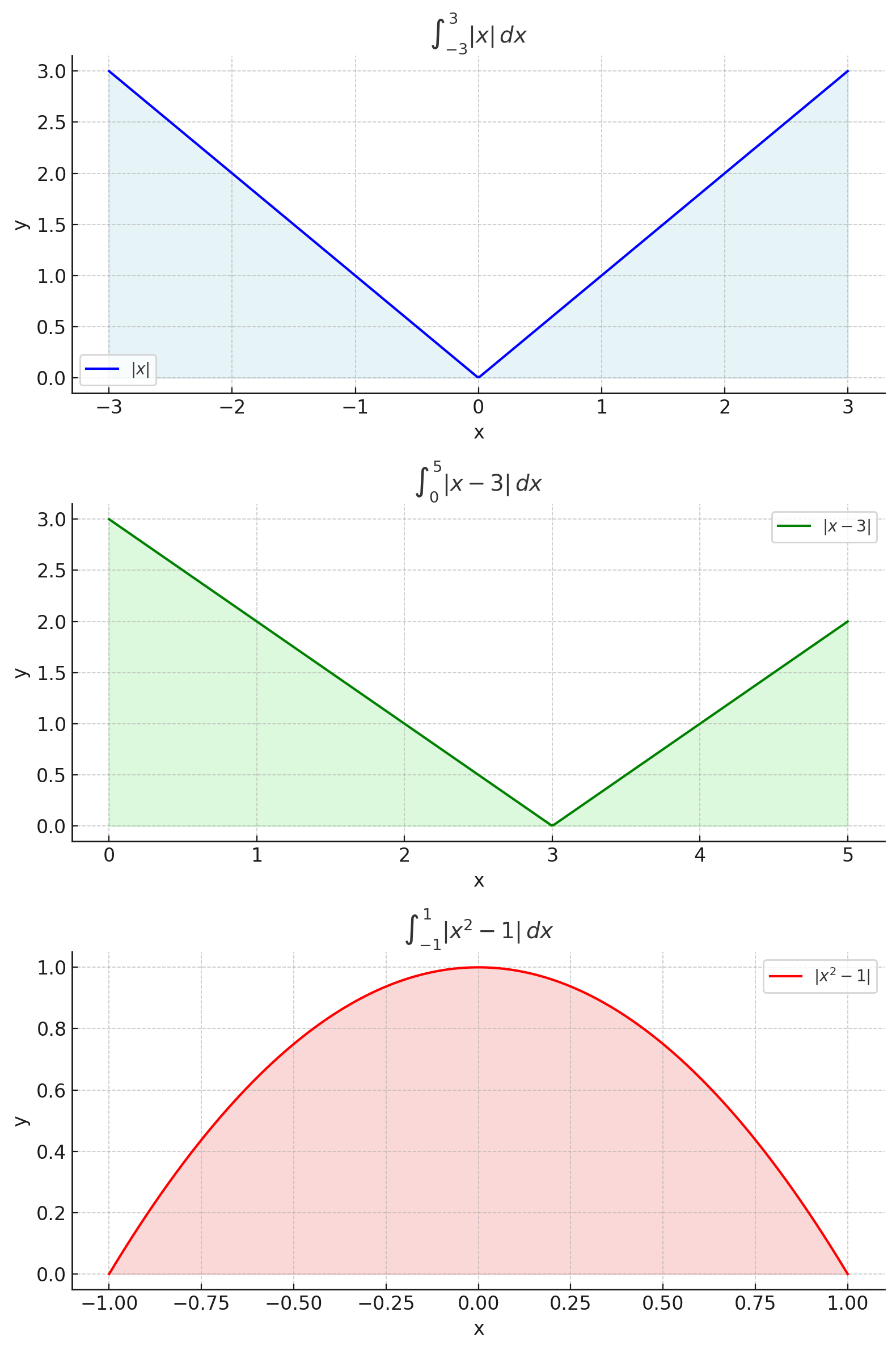
Example 1: $\int |x| \, dx$

Let’s start with a simple example: $\int |x| \, dx$. We know that:

$$|x| = \begin{cases} x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases}$$

Thus, we split the integral into two parts:

$$\int |x| \, dx = \int_{-a}^{0} (-x) \, dx + \int_{0}^{a} x \, dx$$

Now, solve each part:

• For $x < 0$, the integral becomes $\int_{-a}^{0} -x \, dx$, which equals:

  $$\left[ -\frac{x^2}{2} \right]_{-a}^{0} = \frac{a^2}{2}$$

• For $x \geq 0$, the integral becomes $\int_{0}^{a} x \, dx$, which equals:

  $$\left[ \frac{x^2}{2} \right]_{0}^{a} = \frac{a^2}{2}$$

Combining these results gives:

$$\int_{-a}^{a} |x| \, dx = \frac{a^2}{2} + \frac{a^2}{2} = a^2$$

So, the integral of $|x|$ from $-a$ to $a$ is simply $a^2$.

Example 2: $\int |x - 2| \, dx$

Now, let’s work on a slightly more complicated example: $\int |x - 2| \, dx$.

We need to determine where $x - 2 = 0$, which occurs at $x = 2$. This gives us two intervals: $-\infty \leq x < 2$ and $x \geq 2$.

Now, split the integral based on the sign of $x - 2$:

$$|x - 2| = \begin{cases} -(x - 2) & \text{if } x < 2 \\ x - 2 & \text{if } x \geq 2 \end{cases}$$

For an interval $[a, b]$, we write the integral as:

$$\int_{a}^{b} |x - 2| \, dx = \int_{a}^{2} -(x - 2) \, dx + \int_{2}^{b} (x - 2) \, dx$$

This split allows us to solve the integral in two parts, similar to the first example.

Why It’s Important to Master the Integral of Absolute Value

Understanding how to solve the integral of absolute value is essential for several reasons:

1. Versatility in Solving Problems:
   The absolute value function is commonly encountered in many calculus problems, particularly in physics, engineering, and economics. Mastering its integral will help you tackle a wider range of real-world problems.

2. Preparation for Advanced Topics:
   The integral of absolute value is an essential concept that serves as a foundation for more complex integrals, like those involving piecewise functions or integrals with discontinuities.

3. Improve Your SAT, ACT, and AP Calculus Skills:
   The integral of absolute value is a common topic on standardized exams like the SAT, ACT, and AP Calculus exams. Understanding how to handle these integrals will help boost your test-taking confidence and performance.

Example Problems for Practice

Here are a few more problems for you to practice:

Problem 1:

$$\int_{-3}^{3} |x| \, dx$$

Problem 2:

$$\int_{0}^{5} |x - 3| \, dx$$

Problem 3:

$$\int_{-1}^{1} |x^2 - 1| \, dx$$

Conclusion

The integral of absolute value is an important concept that you’ll frequently encounter in calculus. By breaking the problem into intervals where the function inside the absolute value is either positive or negative, you can easily compute the integral. Practice these steps and examples, and soon you’ll be solving these problems with confidence!

If you're preparing for exams, mastering this concept will give you a solid foundation for more advanced topics in calculus and beyond. Keep practicing, and don’t hesitate to revisit these steps if you ever feel stuck!

Try AI Homework Helper to Solve More Integrals!

For students looking for fast and accurate solutions to problems like these, AI Homework Helper is a great tool. It can quickly solve integrals of absolute value and provide step-by-step explanations to help you understand the process. With AI Homework Helper, you can learn smarter and study more effectively.

Happy studying, and best of luck with your calculus journey!

Answers for Example Problems.

Sure! Let’s break down the solutions for each of these problems step by step.

Problem 1:

$$\int_{-3}^{3} |x| \, dx$$

Solution:

First, notice that $|x|$ is a piecewise function:

$$|x| = \begin{cases} x & \text{if } x \geq 0 \\ -x & \text{if } x < 0 \end{cases}$$

Thus, we can split the integral into two parts:

$$\int_{-3}^{3} |x| \, dx = \int_{-3}^{0} -x \, dx + \int_{0}^{3} x \, dx$$

Now, let's calculate each part:

1. For $\int_{-3}^{0} -x \, dx$:

   $$\int_{-3}^{0} -x \, dx = \left[ -\frac{x^2}{2} \right]_{-3}^{0} = -\frac{0^2}{2} + \frac{(-3)^2}{2} = \frac{9}{2}$$

2. For $\int_{0}^{3} x \, dx$:

   $$\int_{0}^{3} x \, dx = \left[ \frac{x^2}{2} \right]_{0}^{3} = \frac{9}{2} - 0 = \frac{9}{2}$$

Now, add the two parts together:

$$\frac{9}{2} + \frac{9}{2} = 9$$

Final Answer:

$$\int_{-3}^{3} |x| \, dx = 9$$

---

Problem 2:

$$\int_{0}^{5} |x - 3| \, dx$$

Solution:

Again, we need to split the absolute value function into two parts. The function $|x - 3|$ changes sign at $x = 3$.

$$|x - 3| = \begin{cases} -(x - 3) & \text{if } x < 3 \\ x - 3 & \text{if } x \geq 3 \end{cases}$$

So, we split the integral into two parts: from 0 to 3 and from 3 to 5:

$$\int_{0}^{5} |x - 3| \, dx = \int_{0}^{3} -(x - 3) \, dx + \int_{3}^{5} (x - 3) \, dx$$

Now, let’s calculate each part:

1. For $\int_{0}^{3} -(x - 3) \, dx$:

   $$\int_{0}^{3} -(x - 3) \, dx = \int_{0}^{3} (-x + 3) \, dx$$ $$= \left[ -\frac{x^2}{2} + 3x \right]_{0}^{3} = \left( -\frac{9}{2} + 9 \right) - (0) = \frac{9}{2}$$

2. For $\int_{3}^{5} (x - 3) \, dx$:

   $$\int_{3}^{5} (x - 3) \, dx = \left[ \frac{x^2}{2} - 3x \right]_{3}^{5}$$ $$= \left( \frac{25}{2} - 15 \right) - \left( \frac{9}{2} - 9 \right)$$ $$= \frac{25}{2} - 15 - \frac{9}{2} + 9 = \frac{16}{2} - 6 = 8 - 6 = 2$$

Now, add the two parts together:

$$\frac{9}{2} + 2 = \frac{9}{2} + \frac{4}{2} = \frac{13}{2}$$

Final Answer:

$$\int_{0}^{5} |x - 3| \, dx = \frac{13}{2}$$

---

Problem 3:

$$\int_{-1}^{1} |x^2 - 1| \, dx$$

Solution:

The expression $|x^2 - 1|$ changes sign when $x^2 = 1$, i.e., when $x = \pm 1$. However, since we are integrating from $-1$ to $1$, the expression $x^2 - 1$ is negative for $-1 \leq x < 0$ and positive for $0 < x \leq 1$.

Thus, we split the integral:

$$|x^2 - 1| = \begin{cases} -(x^2 - 1) & \text{for } -1 \leq x < 0 \\ x^2 - 1 & \text{for } 0 \leq x \leq 1 \end{cases}$$

So, we can write:

$$\int_{-1}^{1} |x^2 - 1| \, dx = \int_{-1}^{0} -(x^2 - 1) \, dx + \int_{0}^{1} (x^2 - 1) \, dx$$

Let’s calculate each part:

1. For $\int_{-1}^{0} -(x^2 - 1) \, dx$:

   $$\int_{-1}^{0} -(x^2 - 1) \, dx = \int_{-1}^{0} (-x^2 + 1) \, dx$$ $$= \left[ -\frac{x^3}{3} + x \right]_{-1}^{0} = \left( 0 + 0 \right) - \left( -\frac{-1^3}{3} + (-1) \right) = \frac{1}{3} + 1 = \frac{4}{3}$$

2. For $\int_{0}^{1} (x^2 - 1) \, dx$:

   $$\int_{0}^{1} (x^2 - 1) \, dx = \left[ \frac{x^3}{3} - x \right]_{0}^{1}$$ $$= \left( \frac{1^3}{3} - 1 \right) - (0) = \frac{1}{3} - 1 = -\frac{2}{3}$$

Now, add the two parts together:

$$\frac{4}{3} + \left( -\frac{2}{3} \right) = \frac{2}{3}$$

Final Answer:

$$\int_{-1}^{1} |x^2 - 1| \, dx = \frac{2}{3}$$

---